Técnicas de IA para Biologia
3 - Activation, Loss and Optimization
André Lamúrias
Introduction
Summary
- The vanishing gradients problem
- ReLU to the rescue
- Different activations: when and how
- Loss functions
- Optimizers
- Overfitting and model selection
- Regularization methods in ANN
Activation, Loss and Optimization
Vanishing gradients
Vanishing gradients
Backpropagation in Activation and Loss
- Output neuron $n$ of layer $k$ receives input from $m$ from layer $i$ through weight $j$ $$\begin{array}{rcl} \Delta w_{mkn}^j&=& - \eta \frac{\delta E_{kn}^j}{\delta s_{kn}^j} \frac{\delta s_{kn}^j}{\delta net_{kn}^j}\frac{\delta net_{kn}^j}{\delta w_{mkn}} &=& \eta (t^j - s_{kn}^j) s_{kn}^j (1-s_{kn}^j) s_{im}^j = \eta \delta_{kn} s_{im}^j \end{array}$$
- For a weight $m$ on hidden layer $i$, we must propagate the output error backwards from all neurons ahead $$\Delta w_{min}^j= - \eta \left( \sum\limits_{p} \frac{\delta E_{kp}^j}{\delta s_{kp}^j} \frac{\delta s_{kp}^j}{\delta net_{kp}^j}\frac{\delta net_{kp}^j}{\delta s_{in}^j} \right) \frac{\delta s_{in}^j}{\delta net_{in}^j}\frac{\delta net_{in}^j}{\delta w_{min}} $$
- If $\delta s$ is small (vanishing gradient) backpropagation becomes ineffective as we increase depth
- This happens with sigmoid activation (or similar, such as TanH)
Vanishing gradients
- Single hidden layer, sigmoid, works fine here

Vanishing gradients
- Single hidden layer, sigmoid, doesn't work here with 8 neurons

Vanishing gradients
- Increasing depth does not seem to help

Vanishing gradients
- Increasing depth does not seem to help

Vanishing gradients
- Increasing depth does not seem to help
- Sigmoid activation saturates and gradients vanish with large coefs.

Activation, Loss and Optimization
Rectified Linear Unit
ReLU
Rectified Linear Unit (ReLU)
- Sigmoid activation units saturate
$$y_i = \frac{1}{1+e^{-x_i}}$$
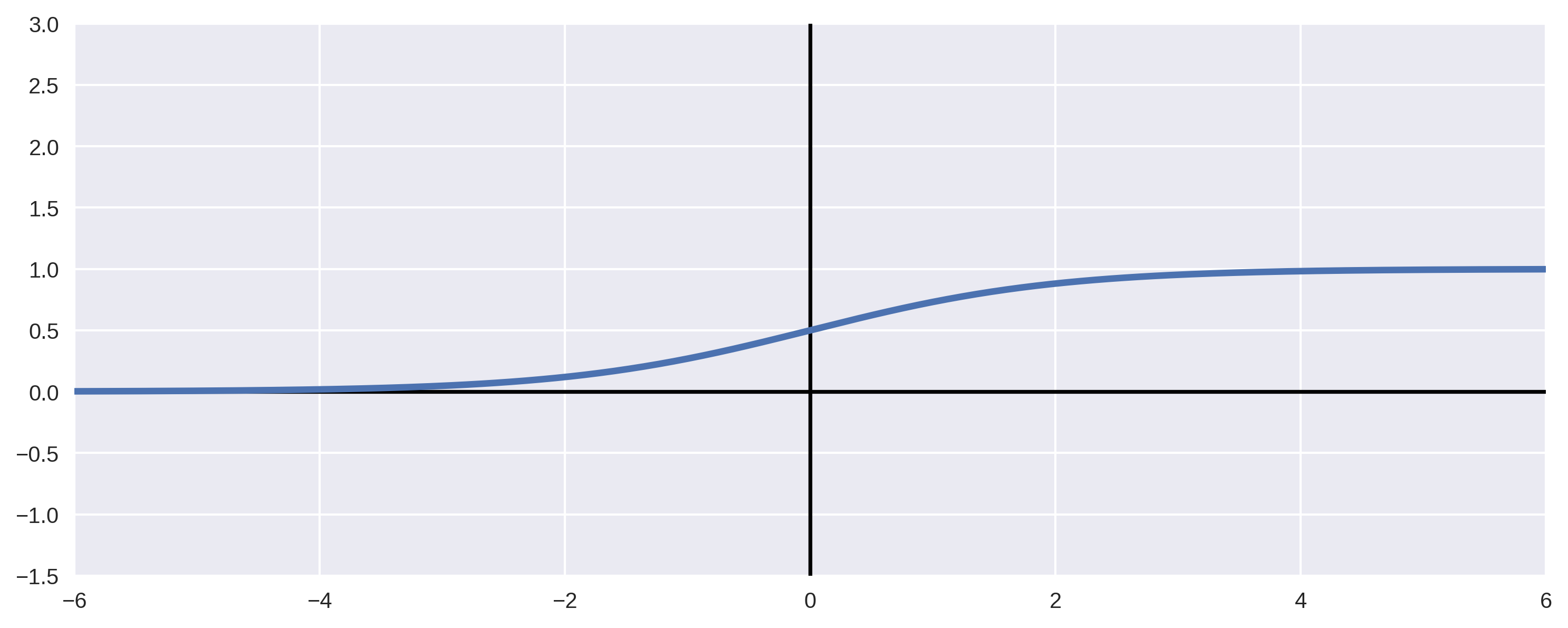
ReLU
Rectified Linear Unit (ReLU)
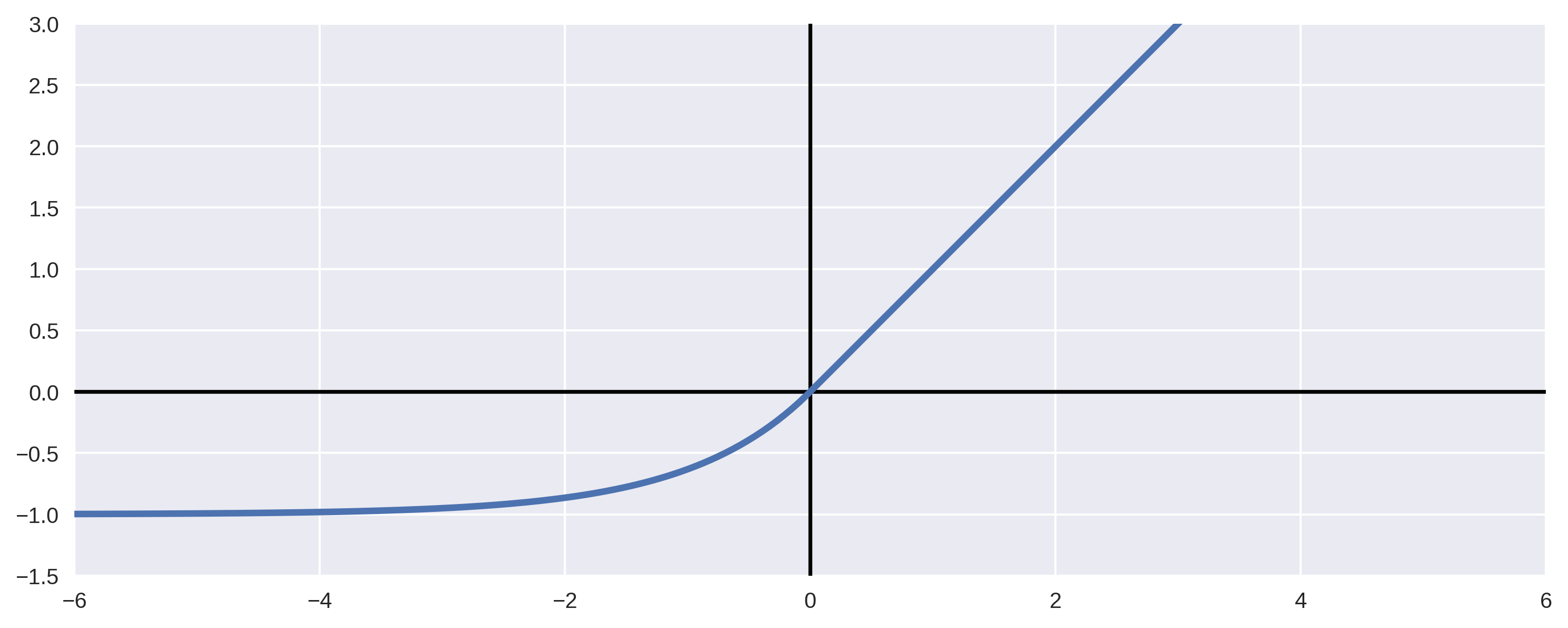
- The same happens with hyperbolic tangent
$$y_i = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

ReLU
Rectified Linear Unit (ReLU)
- Rectified linear units do not have this problem
$$y_i= \left\{ \begin{array}{ll} x_i & x_i \gt 0 \\ 0 & x_i \leq 0 \\ \end{array} \right.$$

ReLU
- Sigmoid activation, 3 layers

ReLU
- ReLU activation, 3 layers

ReLU
- ReLU activation, 4 layers

ReLU
Rectified Linear Unit (ReLU)
- Advantages of ReLU activation:
- Fast to compute
- Does not saturate for positive values, and gradient is always 1
- Disadvantage:
- ReLU units can "die" if training makes their weights very negative
- The unit will output 0 and the gradient will become 0, so it will not "revive"
- There are variants that try to fix this problem
ReLU
(Some) ReLU variants
- Simple ReLU can die if coefficients are negative
$$y_i= \left\{ \begin{array}{ll} x_i & x_i \gt 0 \\ 0 & x_i \leq 0 \\ \end{array} \right.$$

ReLU
ReLU variant: Leaky ReLU
- Leaky ReLU gradient is never 0
$$y_i= \left\{ \begin{array}{ll} x_i & x \gt 0 \\ \frac{x_i}{a_i} & x_i \leq 0 \\ \end{array} \right.$$

ReLU
ReLU variant: Leaky ReLU
- Note: in Tensorflow
$$y_i= \left\{ \begin{array}{ll} x_i & x \gt 0 \\ a_i x_i & x_i \leq 0 \\ \end{array} \right.$$

ReLU
ReLU variant: Parametric ReLU
- Same as leaky, but $a_i$ is also learned
$$y_i= \left\{ \begin{array}{ll} x_i & x \gt 0 \\ \frac{x_i}{a_i} & x_i \leq 0 \\ \end{array} \right.$$

ReLU
ReLU variant: Randomized Leaky ReLU
- Similar, but $a_i \sim U(l,u)$ (average of $l,u$ in test)
$$y_i= \left\{ \begin{array}{ll} x_i & x \gt 0 \\ a_i x_i & x_i \leq 0 \\ \end{array} \right.$$

ReLU
Comparing ReLU variants
Empirical Evaluation of Rectified Activations in Convolution Network (Xu et. al. 2015)
- Compared on 2 data sets
- CIFAR-10: 60000 32x32 color images in 10 classes of 6000 each
- CIFAR-100: 60000 32x32 color images in 100 classes of 600 each


CReLU
- Concatenated ReLU combine two ReLU for $x$ and $-x$ $$y_i= \left\{ \begin{array}{ll} x_i & x_i \gt 0 \\ 0 & x_i \leq 0 \\ \end{array} \right. \qquad z_i= \left\{ \begin{array}{ll} 0 & x_i \gt 0 \\ -x_i & x_i \leq 0 \\ \end{array} \right.$$

Shang et. al., Understanding and Improving CNN via CReLUs, 2016
ELU
Exponential Linear Unit
- Exponential in negative part
$$y_i= \left\{ \begin{array}{ll} x_i & x_i \gt 0 \\ a(e^{x_i}-1) & x_i \leq 0 \\ \end{array} \right.$$
Clevert et. al. Fast and Accurate Deep Network Learning by ELUs, 2015
Activation, Loss and Optimization
Activations: which, when, why?
Choosing activations
Hidden layer activations
- Hidden layers perform nonlinear transformations
- Without nonlinear activation functions, all layers would just amount to a single linear transformation
- Activation functions should be fast to compute
- Activation functions should avoid vanishing gradients
- This is why ReLU (esp. leaky variants) are the recommended choice for hidden layers
- Except for specific applications.
- E.g. LSTM, Long short-term memory recurrent networks
Choosing activations
Output layer activations
- Output layers are a different case.
- Choice depends on what we want the model to do
- For regression, output should generally be linear
- We do not want bounded values and there is little need for nonlinearity in the last layer
- For binary classification, sigmoid is a good choice
- The output value $[0,1]$ is useful as a representation of the probability of $C_1$, like in logistic regression
- Sigmoid is also good for multilabel classification
- One example may fit with several labels at the same time
- Use one sigmoid output per label
Choosing activations
Output layer activations
- For multiclass classification, use softmax:
- Note: multiclass means each example fits only one of several classes $$\sigma:\mathbb{R}^K \rightarrow [0,1]^K \qquad \sigma(\vec{x})_j= \frac{e^{x_j}}{\sum\limits_{k=1}^K e^{x_k}}$$
- Softmax returns a vector where $\sigma_j \in [0,1]$ and $\sum\limits_{k=1}^K \sigma_k = 1$
- This can fit a probability of example belonging to each class $C_j$
- Softmax is a generalization of the logistic function
- It combines the activations of several neurons
Activation, Loss and Optimization
Loss and likelihood
Likelihood
Basic concepts
- We have a set of labelled data $$\left\{(\vec{x}^1,y^1), ..., (\vec{x}^n,y^n)\right\}$$
- We want to approximate some function $F(X) : X \rightarrow Y$ by fitting our parameters
- Given some training set, what are the best parameter values?
Simple example, linear regression
$$y = \theta_1 x_1 + \theta_2 x_2 + ... + \theta_{n+1}$$- We have a set of $(x,y)$ examples and want to fit the best line: $$y = \theta_1 x + \theta_2$$
Likelihood
What to optimize?

Likelihood
What to optimize?
- Assume $y$ is a function of $x$ plus some error: $$ y = F(x) + \epsilon $$
- We want to approximate $F(x)$ with some $g(x,\theta)$
- Assuming $\epsilon \sim N(0,\sigma^2)$ and $g(x,\theta) \sim F(x)$, then: $$p(y|x)\sim\mathcal{N}(g(x,\theta),\sigma^2) $$
- Given $\mathcal{X}=\{ x^t,y^t \}_{t=1}^{N}$ and knowing that $p(x,y)=p(y|x)p(x)$ $$p(X,Y)=\prod_{t=1}^{n}p(x^t,y^t)= \prod_{t=1}^{n}p(y^t|x^t)\times\prod_{t=1}^{n}p(x^t)$$
Likelihood
What to optimize?
- The probability of $(X,Y)$ given $g(x,\theta)$ is the
likelihood of $\theta$:
$$l(\theta|\mathcal{X})=\prod_{t=1}^{n}p(\vec{x}^t,y^t)= \prod_{t=1}^{n}p(y^t|x^t)\times\prod_{t=1}^{n}p(x^t)$$
Likelihood
- The examples $(\vec{x},y)$ are randomly sampled from all possible values
- But $\theta$ is not a random variable
- Find the $\theta$ for which the data is most probable
- In other words, find the $\theta$ of maximum likelihood
Likelihood
Maximum likelihood for linear regression
$$l(\theta|\mathcal{X})=\prod_{t=1}^{n}p(x^t,y^t)= \prod_{t=1}^{n}p(y^t|x^t)\times\prod_{t=1}^{n}p(x^t)$$- First, take the logarithm (same maximum) $$L(\theta|\mathcal{X})=log\left(\prod_{t=1}^{n}p(y^t|x^t)\times\prod_{t=1}^{n}p(x^t)\right)$$
- We ignore $p(X)$, since it's independent of $\theta$ $$L(\theta|\mathcal{X}) \propto log\left(\prod_{t=1}^{n}p(y^t|x^t)\right)$$
- Replace the expression for the normal distribution: $$\mathcal{L}(\theta|\mathcal{X})\propto log\prod_{t=1}^{n}\frac{1}{\sigma \sqrt {2\pi } } e^{- [y^t - g(x^t|\theta)]^2 /2\sigma^2 }$$
Likelihood
Maximum likelihood for linear regression
$$\mathcal{L}(\theta|\mathcal{X})\propto log\prod_{t=1}^{n}\frac{1}{\sigma \sqrt {2\pi } } e^{- [y^t - g(x^t|\theta)]^2 /2\sigma^2 }$$- Simplify: $$\mathcal{L}(\theta|\mathcal{X})\propto log\prod_{t=1}^{n}e^{- [y^t - g(x^t|\theta)]^2}$$ $$\mathcal{L}(\theta|\mathcal{X})\propto -\sum_{t=1}^{n} [y^t - g(x^t|\theta)]^2$$
Likelihood
Maximum likelihood for linear regression
$$\mathcal{L}(\theta|\mathcal{X})\propto -\sum_{t=1}^{n} [y^t - g(x^t|\theta)]^2$$- Max(likelihood) = Min(squared error)
- Note: the squared error is often written like this for convenience: $$E(\theta|\mathcal{X})=\frac{1}{2}\sum_{t=1}^{n} [y^t - g(x^t|\theta)]^2$$
Likelihood
- Having the Loss function, we do gradient descent

Likelihood
- Having the Loss function, we do gradient descent
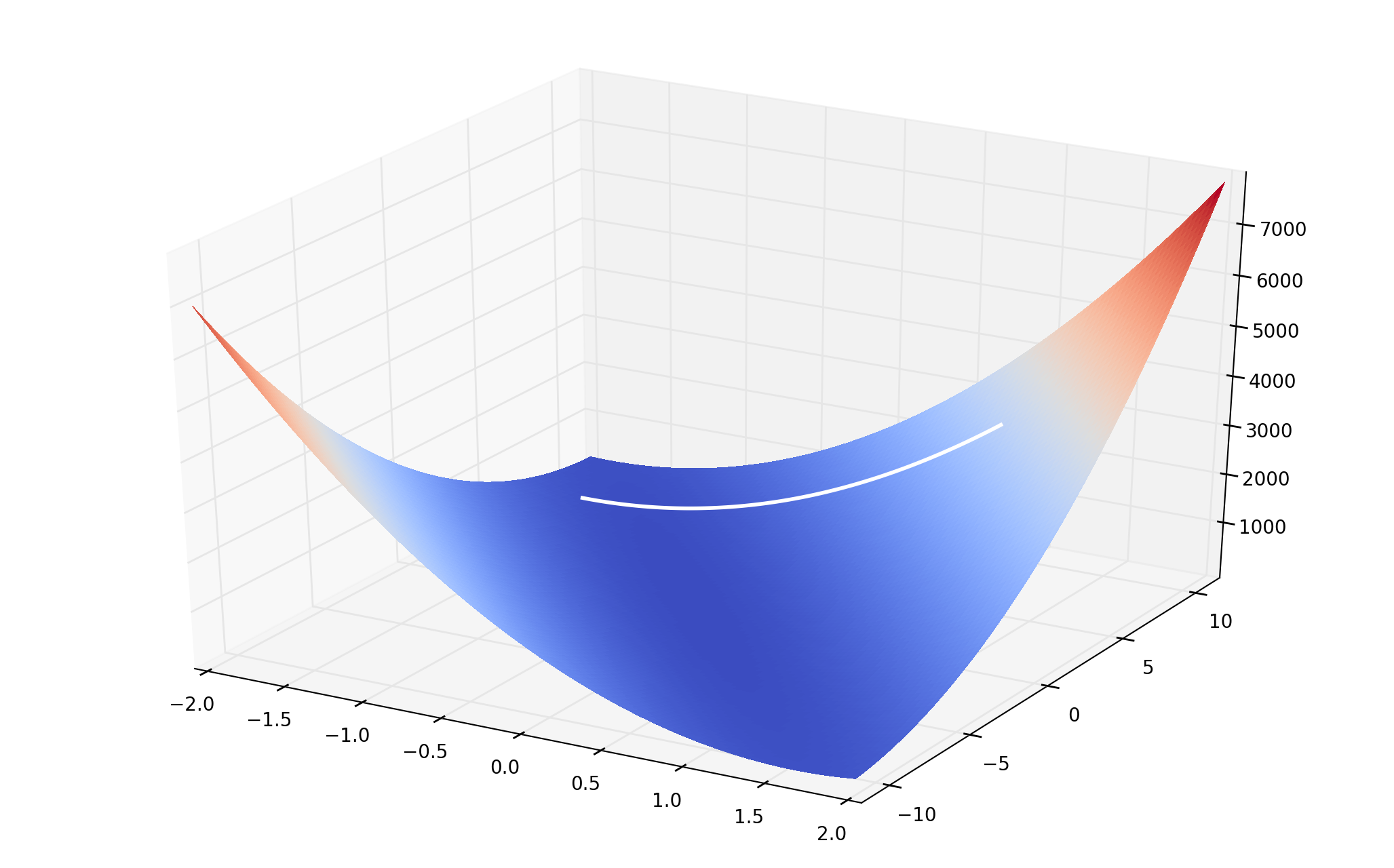
Likelihood
- Having the Loss function, we do gradient descent
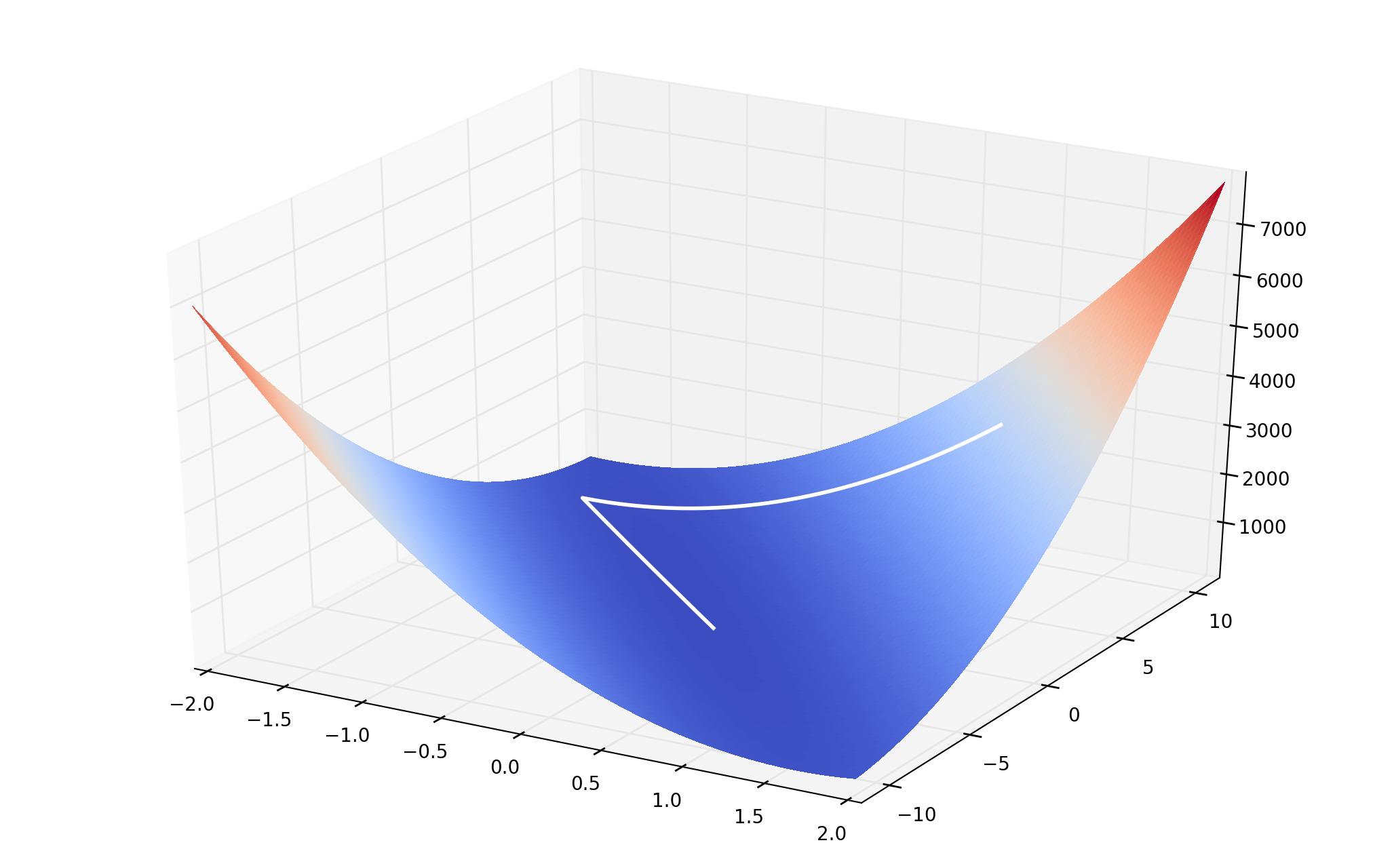
Maximum Likelihood
Finding a loss function by ML
$$\theta_{ML} = \underset{\theta}{\operatorname{arg}\,\operatorname{max}}\;P(Y|X;\theta) = \underset{\theta}{\operatorname{arg}\,\operatorname{max}}\;\sum\limits_{i=1}^{m}\operatorname{log}\,P(y^i|\vec{x}^i;\theta)$$- We want to maximize likelihood
- This means minimizing cross entropy between model and data
- Loss function depends on the model output:
- Regression: linear output, mean squared error
- Binary classification: class probability, sigmoid output, logistic loss
- (Also for multilabel classification, with probability for each label)
- N-ary classification, use softmax and the softmax cross entropy: $$-\sum\limits_{c=1}^{C} y_c \operatorname{log}\frac{e^{a_c}}{\sum_{k=1}^{C} e^{a_k}}$$
Activation, Loss and Optimization
Optimizers
Optimizers
Minimizing the loss function
- We want to minimize the loss function (e.g. cross-entropy for ML) to obtain $\theta$ from some data
- Numerical optimization is outside the scope of this course
- But it's useful to have some knowledge of the optimizers
Optimizers
Minimizing the loss function
- So far we saw
tf.optimizers.SGD - Basic gradient descent algorithm, single learning rate.
- Stochastic gradient descent: use gradient computed at each example, selected at random
- Mini-batch gradient descent: updates after computing the total gradient from a batch of randomly selected examples.
- Can include momentum (and you should use momentum, in general)
- This is just an alias for the
tf.keras.optimizers.SGDclass - We'll be using Keras explicitely from now on
Optimizers
Minimizing the loss function:
- Different parameters may best be changed at different rates
-
tf.keras.optimizers.Adagrad - Keeps sum of past (squared) gradients for all parameters
- Divides learning rate of each parameter by this sum
- Parameters with small gradients will have larger learning rates, and vice-versa
- Since Adagrad sums previous gradients, learning rates will shrink
- (good for convex problems)
Optimizers
Minimizing the loss function:
- Some parameters may be left with too large or too small gradients
-
tf.keras.optimizers.RMSProp - Keeps moving root of the mean of the squared gradients (RMS)
- Divides gradient by this moving RMS
- Updates will tend to be similar for all parameters.
- Since it uses a moving average, learning rates don't shrink
- Good for non-convex problems, and often used in recurrent neural networks
- Most famous unpublished optimizer
Optimizers
Minimizing the loss function
-
tf.keras.optimizers.Adam - Adaptive Moment Estimation (Adam)
- Momentum and different learning rates using an exponentially decaying average over the previous gradients
-
tf.keras.optimizers.AdamW - Adaptive Moment Estimation (Adam)
- Similar to Adam but with Weight Decay, generalizes better than Adam
- Fast to learn but may have convergence problems
How to choose?
- There is no solid theoretical foundation for this
- So you must choose empirically
- Which is just a fancy way of saying try and see what works...
Learning Rate
Choosing the best learning rate
- Optimizers can have other parameters, but all have a learning rate
- Too high a learning rate can lead to convergence problems

Learning Rate
- However, if learning rate is too small training can take too long
- Try to make it as high as you can while still converging to low error
- (you can experiment with a subset of your training set, even if overfitting)
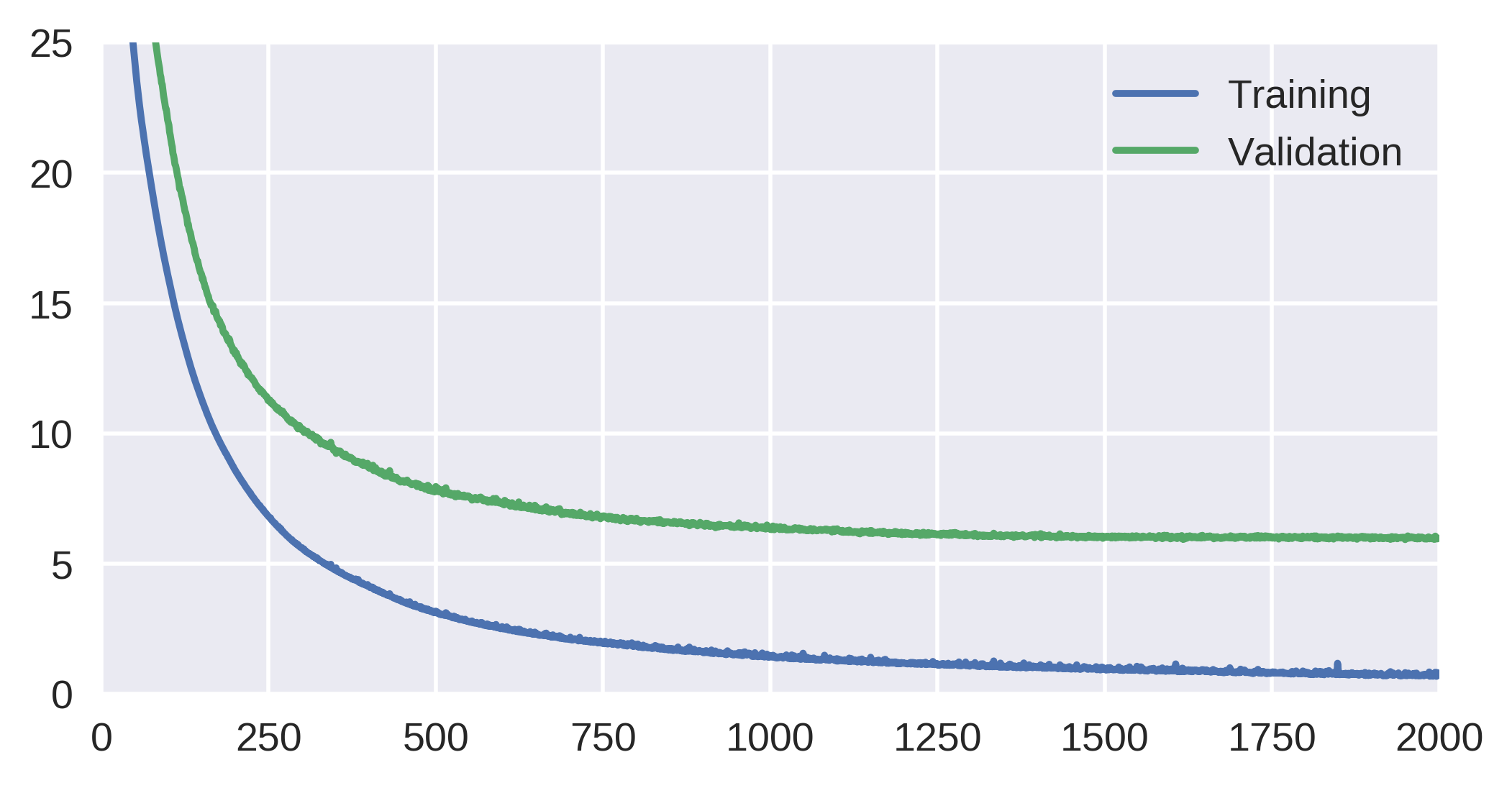
Batch Normalization
Normalizing (standardizing) activations
- Compute running averages and standard deviations during training
- And standardize the inputs to each layer
- Just like we do for the inputs to the network, do for hidden layers too
- Makes learning easier by preventing extreme values
- Eliminates shifts in mean and variance during training
- Reduces the need for each layer to adapt to the changes in the previous one
- This can be done easily in Keras
- The mean, standard deviation and rescaling can all be part of backpropagation
- AutoDiff takes care of the derivatives
- So we can add batch normalization as an additional layer
Activation, Loss and Optimization
Overfitting and Validation
Overfitting and Validation
The goal of (supervised) learning is prediction
- And we want to predict outside of what we know
Overfitting
- The problem of adjusting too much to training data
- and losing generalization
- Two ways of solving this:
- Select the right model: model selection
- Adjust training: regularization
Overfitting and Validation
How to check for overfitting
- We need to evaluate performance outside the training set
- Test set: we need to keep this for final evaluation of error rate
- We can use a validation set
- Or we can use cross-validation
Overfitting and Validation
How to check for overfitting
- Cross-Validation:
- Split training set into K folds, average validations training on the k-1


Overfitting and Validation
How to check for overfitting
- Cross-Validation:
- Split training set into K folds, average validations training on the k-1


Overfitting and Validation
How to check for overfitting
- Option 1: Cross-validation on training set, test
- Good when data is scarcer
- Better estimate of true error
- More computationally demanding
- Option 2: train, validation for preventing overfitting, test
- Good when we have lots of data (which is generally the case for DL)
- Cross-validation is widely used outside deep learning
- With deep learning training and validation is more common
- Deep networks take some time to train
Overfitting and Validation
Estimating the true error
- True error: the expected error over all possible data
- We cannot measure this, since we would need all possible data
- Must be estimated with a test set, outside the training set
- This cannot be the validation set if the validation set was used to optimize hyperparameters
- We choose the combination with the smallest validation error, this makes the estimate biased.
- Solution: reserve a test set for final estimate of true error
- This set should not be used for any choice or optimization
Overfitting
Model Selection
- If the model adapts too much to the data, the training error may be low but the true error high
- Example: Auto MPG problem, 100-50-10-1 network.

Overfitting
Model Selection
- One way of solving this problem is to use a simpler model (assuming it can fit the data)
- Example: Auto MPG problem, 30-10-1 network.

Overfitting
Model Selection
- If the model is too simple, then error may become high
- (Underfitting)
- Example: Auto MPG problem, 3-2-1 network.

Activation, Loss and Optimization
Regularization in ANN
Regularization
Penalizing parameter size
- To reduce variance, we can force parameters to remain small by adding a penalty to the objective (cost) function: $$\tilde J(\theta;X,y) = J(\theta;X,y) + \alpha \Omega(\theta)$$
- Where $\alpha$ is the weight of the regularization
- Note: in ANN, generally only the input weights at each neuron are penalized and not the bias weights.
- The norm function $\Omega(\theta)$ usually takes these forms:
- L$^2$ Regularization (ridge regression): penalize $||\theta||^2$
- L$^1$ Regularization: penalize $\sum_i |\theta_i|$
Regularization
L$^2$ Regularization is weight decay
- If we penalize $w^2$, the gradient becomes: $$\nabla \tilde J(\theta;X,y) = \nabla J(\theta;X,y) + 2\alpha w$$
- This means the update rule for the weight becomes $$w \leftarrow w - \epsilon 2\alpha w - \epsilon \nabla J(\theta;X,y)$$
- We decrease the magnitude of $w$ to $(1-\epsilon 2 \alpha)$ per update
- This causes weights that do not contribute to reducing the cost function to shrink
Regularization
L$^1$ Regularization
- If we penalize $|w|$, the gradient becomes: $$\nabla \tilde J(\theta;X,y) = \nabla J(\theta;X,y) + \alpha \ sign(w)$$
- This penalizes parameters by a constant value, leading to a sparse solution
- Some weights will have an optimal value of 0
L$^1$ vs L$^2$ Regularization
- L$^1$ minimizes number of non-zero weights
- L$^2$ minimizes overall weight magnitude
Regularization
Dataset augmentation
- More data is generally better, although not always readily available
- But sometimes we can make more data
- E.g. Image classification:
- Translate images. Rotate or flip, if appropriate (not for character recognition)

Wang et al, 2019, "A survey of face data augmentation".
Regularization
Dataset augmentation by noise injection
- Noise injection is an (implicit) form of dataset augmentation
- Add (carefully) noise to inputs, or even to some hidden layers
- Noise can also be applied to the weights
- Or even the output
- There may be errors in labelling
- Or for label smoothing: use $\frac{\epsilon}{(k-1)}$ and $1-\epsilon$ instead of 0 and 1 for target
- This prevents pushing softmax or sigmoid to infinity
Regularization
Early stopping
- Use validation to stop at best point
- Constrains weights to be closer to starting distribution

Regularization
Bagging
- Training a set of models on different subsets of the data
- use the average response (or majority vote)
- Improves performance, as it reduces variance without affecting bias, and ANN can have high variance
- However, it can be costly to train and use many deep models.
Regularization
Dropout
- "Turns off" random input and hidden neurons in each minibatch

Regularization
Dropout
- Dropout does model averaging implicitely
- Turning off neurons at random trains an ensemble of many different networks
- After training, weights are scaled by the probability of being "on"
- (same expected activation value)
- Keras automatically adjust for this when we use a Dropout layer
Activation, Loss and Optimization
Summary
Activation and Loss
Summary
- The vanishing gradients problem, ReLU
- Activations for hidden and output layers
- Loss functions
- Optimizers, learning rate, batch normalization
- Model selection and Regularization
Further reading:
- Goodfellow et.al, Deep learning, Chaps 5-7 and 11, Sects 8.4; 8.7.1
- Tensorflow, activation functions:
- https://www.tensorflow.org/api_guides/python/nn#Activation_Functions